
はじめに
本記事では、コード(和音)の心地よさと、音を波として見た時の「倍音」の概念がどのように関係するかどうかを説明していきます。
先日、以下の記事で、コードの響きを明るいとか暗いとか感じる理由として倍音の概念があるということをちらっとだけ述べましたが、その記事では詳しい説明はしていませんでした。
今回は、倍音とはそもそも何を意味するのか、を述べた上で、それがコードの響きとどのように関連しているかを述べて行こうかと思います。コード理論に興味がある人だけでなく、「倍音ってなんぞや?」と思った方にも読んでいただけるようにしたつもりなので、ぜひ興味がある方は読んでみてください。
倍音とは?
倍音について説明する前に、音の波について簡単に説明しようと思います。音というのは、空気が振動をした時にその揺れが耳に伝わって感じるものです。たとえば、ゴムや紐か何かの両端を固定して真ん中をはじくと、音が鳴るとともにその紐が小刻みに揺れるかと思います。その揺れが空気に伝わったものが音の正体なのです。
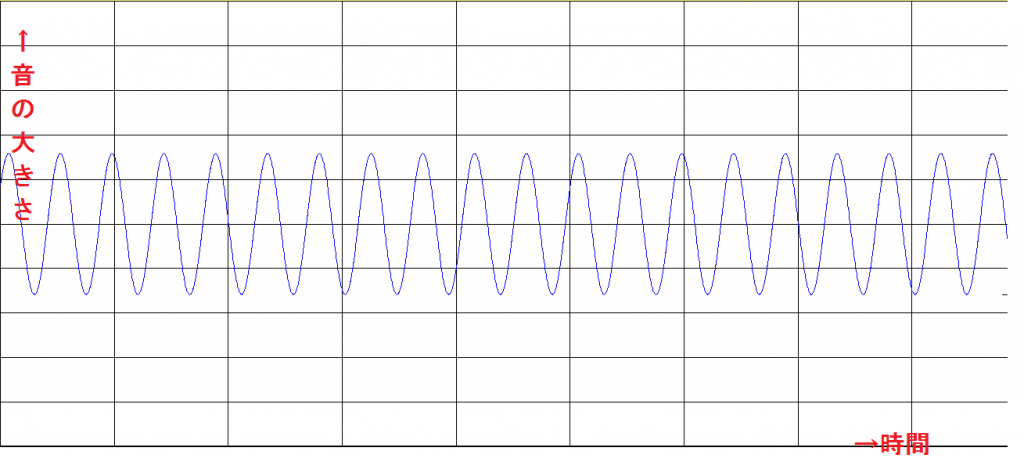
音の波を簡単な模式図で表すと、上の図のようなものになります。これはサインカーブなどと呼ばれ、高校数学でも習う三角関数のグラフそのものです。横軸が時間で、縦軸が空気の振動する大きさを示します。
波の高さは振幅と呼ばれ、「音の大きさ」に相当します。一方、波がどれだけたくさん振動しているか、すなわち、一定の幅の中に何個の波があるか、という量は「周波数」と呼ばれ、「音の高さ」に相当します。周波数が大きいほど高く、周波数が低いほど低い音になります。
たとえば、ピアノの真ん中辺にある「ラ」の高さの音であれば、周波数は440ヘルツであり、これは横軸を0秒から1秒まで取れば、その間に波が440個あることを示します。
しかし、自然界にある音や多くの楽器が出す音は、こんな単純なものではありません。たとえばピアノで「ラ」を弾いた場合、上のような単純なサインカーブにはならず、下のような波になります。
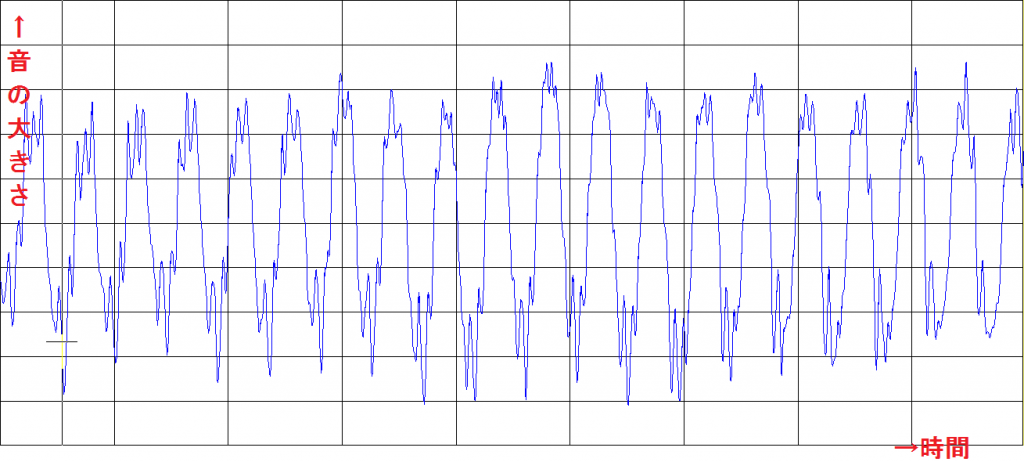
周期性はみられるものの、先ほどのサインカーブに比べるとだいぶ複雑な波に見えます。何故このような複雑な形になるのでしょうか?
それは、楽器が奏でる「ラ」には、周波数が440以外の波もいっぱい混ざっているからなのです。「ラ」の場合、メインは周波数が440の波なのですが、たとえば、メインの波の振幅(大きさ)を100とすれば、周波数が880ヘルツの波が振幅80くらいで、1320ヘルツの波が振幅70くらい…といった具合で、メインの波ほどは大きい音ではないものの、それ以外の周波数(高さ)の音が少しずつ混ざり合っています。その結果、単純なサインカーブではなく、それらを全て合わせた複雑な波形になってしまうのです。
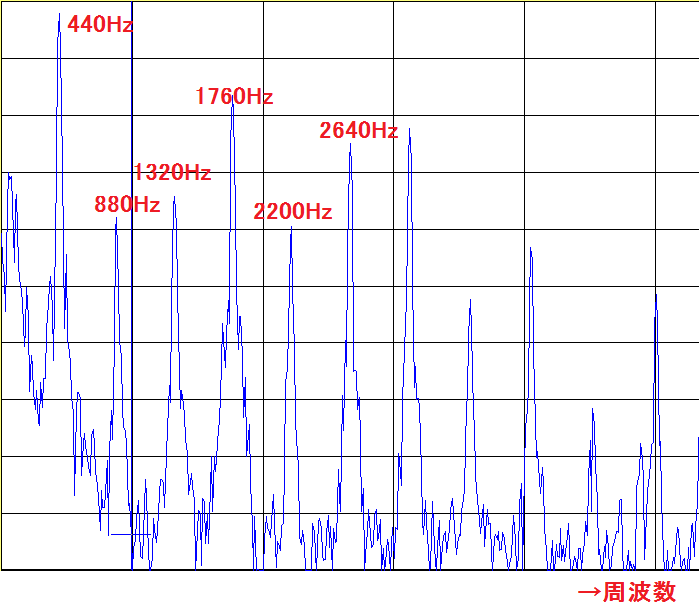
上の図は、ピアノの「ラ」の音を周波数ごとのグラフにしたものです。最初に示したグラフが、時間ごとに空気の波がどのように振動しているかのグラフだったのに対して、こちらのグラフは、どの周波数の音がどの程度ずつ混ざっているものかを表すものになっています。時間ごとのグラフを周波数ごとのグラフに変換する方法は「フーリエ変換」と言い、大学数学の知識が必要なので詳細は省きますが、とにかくこの方法により、色んな高さの音が混ざった音を、音の高さごとに分離して解析することができるのです。
このグラフから、ピアノの「ラ」の音は、周波数が440Hzの音が一番強く出ていますが、それ以外にも880Hz, 1320Hz, …などの音もそれなりの割合で含まれていることがわかります。ちなみに、下の方のギザギザとした部分はノイズであり、音色にはほぼ影響はありません。
どの周波数の音がどのくらいずつ混ざっているかというのは、楽器によって異なります。というより、この割合が違うからこそ、同じ高さであっても多種多様な楽器の音色が存在しているのです。(実際には音色を決める要素は、これだけではありません。楽器を奏でてからの音の減衰しかただったり、弾いた瞬間に鳴る摩擦によるの音等も含めて、その楽器の音色と言えます)。
そして、打楽器を除く多くの楽器の場合、その混ざり合う音の周波数は元の音の整数倍のものがほとんどです。上のグラフでも、グラフの頂点における周波数は、440の倍数になっていることがわかります。逆に、元の音の整数倍でない波で振幅の大きなものがたくさん混ざっている場合、それはもはや「音程」ではなくただの「音」としか聞こえません。たとえば、机を叩いたり、打楽器を鳴らした時に、その音が「ラ」か「シ」かなんて普通はわかりませんが、これは「ラ」や「シ」の音が決して含まれていないということではなく、440ヘルツの音が100、441ヘルツの音が80、442ヘルツの音が60…といった具合に、色々な音が含まれ過ぎていてどれがメインなのかを判断できないからなのです。ピアノの鍵盤を黒鍵盤も含めてすべて同時に押したらめちゃくちゃな音に聞こえますが、それと同じイメージです(中にはそういった音ですら音程を判別できる、ものすごい絶対音感の持ち主もいるようですが…)。
そして、ようやく本題ですが、メインとなる音が440ヘルツの波だったとして、それに対して880ヘルツや1320ヘルツのように、波の周波数が元の音の整数倍になるような音のことを、「倍音」と呼びます。これに対して、元の音(440ヘルツの音)のことを、「基音」と言います。「倍音」の中でも、基音の2倍の周波数を持った音を「2倍音」、3倍の周波数の音を「3倍音」等と呼びます。上で述べた例は、基音がピアノの中心の「ラ」の場合でしたが、基準としているのが「ド」なら基音の周波数は約523ヘルツで、その2倍音は約1046ヘルツと言った具合に、どの音について議論しているかによって「基音」や「倍音」の周波数はそれぞれ変わってきます。
楽器を弾いたときの音というのは、基音をメインとして倍音も適度に混ざり合った波であり、その倍音がどのように混ざり合っているかの違いこそが、楽器ごとの音色の違いを決定づけているのです。グラフで見ると倍音もそれなりに大きな音が出ているように見えるかもしれませんが、実際には基音に比べると、意識して聞こえるほどの大きさではありません。
しかし、単独で倍音を聞きわけることはできずとも、倍音が全くない音と倍音がたくさん含まれる音では、全く異なるように聞こえるのです(倍音がほとんど含まれてない音とは、最初に挙げたサインカーブのような音で、ブザーのような単調な音です。ピアノの「ラ」と音程は同じでも音色は全然違うと感じます)。倍音は、料理でいう調味料に似ています。料理を食べて、どのような調味料がどのぐらいの量だけ使われたかを判断するのは難しいでしょう。しかし、調味料が全く使われていなかったらその料理はおいしいとは思えないかもしれません。「倍音」も同じで、「鳴っているかどうかはわからないけど、それがなかったらつまらない音になる」、というように、音における隠れたスパイス的な意味合いがあるのです。
倍音は楽器だけでなく、人間の声にも含まれています。歌が上手い人の声を聴いて「倍音の響きが素晴らしい」などと言うことがありますが、これは倍音がいい具合に混ざり合って、多くの人にとって聞き心地がいい声を持っていることを意味します(うらやましいですね)。
2倍音はオクターブ上の音
では、倍音がコードの響きとどのように関係しているのでしょうか?そのことを説明するにあたり、周波数の、音程における非常に重要な事実があります。それは、「周波数が2倍になると、音程は1オクターブ上がる」ということです。オクターブについても一応説明しますと、「ドレミファソラシド」でいうところの、最初の「ド」と最後の「ド」の関係を言います。オクターブ関係にある基音と2倍音は、「高さは違うけど、同じ音」という感覚で聴こえるのが特徴です。これを論理だけで説明するのは大変なので、カラオケを例にして説明したいと思います。
カラオケで、男性が女性の曲を歌う時に、「オクターブ下」で歌うことが良くあります。女性が男性曲を「オクターブ上」で歌うこともありますね。この際、聴いている人は「キーが低いな」あるいは「キーが高いな」と感じることはあっても「音が外れている」という感覚は持ちません。オクターブ下で歌うということは、全ての音において、原曲のボーカルの周波数の1/2で歌うということを意味しますが、そのようなことをしても音痴だとは思わないのは、オクターブ上、あるいはオクターブ下の音が、元の音と「同じ音」という感覚を持つからなのです。
もし、これがオクターブ下ではなくて、伴奏はそのままなのにメロディーだけ「半音下」で歌ったとしたらどうでしょうか?おそらく、ものすごい音痴に聞こえてしまうでしょう。単純に周波数の値だけで着目すれば、オクターブ下よりも半音下の方が、周波数のずれはずっと少ないのですが、周波数が倍(あるいは半分)の関係にある2つの音というのは、それだけ「同じ音」であるという感覚を強く持てる関係にあるのです。
先日の記事で、コードを奏でた時の感じ方は、生まれた環境により異なるかもしれないということを書きましたが、オクターブに限っていえば、どの民族であろうと感じ方は変わりありません。西洋音楽とかけ離れた民族音楽に慣れている人であっても、周波数が2倍(あるいは半分)の音は、元の音と同じという感覚を持ちます(これがなぜかというのは、生物学的な解析が必要であり、理由はよくわかっていないのですが、おそらく数学的に見て、周波数が1:2の波どうしというのは、最も重ね合わせがしやすく、調和がとれているからではないかと思います。)
では、3倍音、4倍音についてはどうでしょうか?1オクターブ上の音が2倍音であれば、2オクターブ上の音が3倍音なのでは?と思われた方がいらっしゃるかもしれません。しかし、それは間違いです。オクターブが1個あがるごとに周波数が2倍になるので、オクターブが2個上がったら、周波数は2×2で4倍になります。
上のグラフでいうと、1760ヘルツの部分が4倍音に相当し、元の「ラ」の2オクターブ上の「ラ」ということになります。当然、2オクターブ上の音も、元の音とは高さこそかけ離れていますが、「同じ音」であるように聞こえます。
倍音と音程の関係
それでは、周波数が3倍の音はどうでしょうか?たとえば、440ヘルツの「ラ」の場合、3倍音の周波数は1320ヘルツになります。そして、1320ヘルツの音というのは、音階でいうと「ミ」の音に当たります。
先ほどの2倍音や4倍音のようにオクターブ関係にある音とは違い、元の音と3倍音は、人間の耳に、はっきりと「違う音」として認識されます。当然ですよね、「ラ」と「ミ」が同じ音と思う人はいないでしょう。
ただし、これらは周波数が他方の3倍という単純な整数比にある関係であることから、同時に鳴らした場合に、(オクターブ感の2音ほどではないですが)非常に心地いい感触として聴くことができます。そのことから、多くの音楽コードでは、基音に対して3倍音と同等の音を含むコードが非常に多いです。例えば、AメジャーもAマイナーも、Eの音を含んでますよね?また、ギターの「パワーコード」と言われるものも、「ラミ」や「ドソ」等、基音とその3倍音(のオクターブ下の音)との組み合わせです。基音と3倍音の関係はの和音は、楽曲のいたるところで自然に使われているのです。
4倍音は先に述べたように、基音から2オクターブ上の音でした。では、周波数が5倍の音はどのような音でしょうか?基音が440ヘルツの「ラ」の場合、5倍音の周波数は2200ヘルツで、これは「ド#」の音に相当します。
基音と5倍音の2音を同時に鳴らした場合も、多くの人は調和のとれた心地よい響きに聞こえると思います。そして、「ラ」が基音であり、「ド#」が同時に鳴る和音と言うのは、Aメジャーに他なりません。Aメジャーコードは、「ラ」「ド#」「ミ」の3音から構成されており、「ラ」の音を基準にすると、3倍音である「ミ」と5倍音である「ド#」が同時に鳴っていることになります。
前回の記事で「メジャーコードが明るい理由」として倍音にその秘密があるといったものの詳しい説明は端折っていましたが、それは、「基音と3倍音」および「基音と5倍音」の関係で構成されていることが大きな理由だったわけです。
更に周波数の大きな倍音も見ていきましょう。6倍音は、3倍音の2倍なので、3倍音と同じく「ミ」です。では、7倍音はどの高さの音になるのでしょうか?
基音が「ラ」の場合、その7倍音はおおよそ「ソ」くらいの音になります。おおよそというのは、「ラ」の7倍音に関してはピアノなどで「ソ」を弾いた時の音程よりも半音の更に半音くらい低く、普通の楽器で出せるどの音にも該当しないからです。この音を基音の「ラ」と同時に鳴らした場合、(特に西洋音楽に慣れていて、音感が良い人ほど)気持ち悪い感じを受けることが多いようです。しかし、先ほども述べたように倍音というのはスパイスみたいな存在なので、7倍音のような音は意識してもまず聞き取れることはなく、ピアノで「ラ」を弾いても7倍音のせいで不自然に感じることはないわけです。(実は、7倍音に限らず、3倍音や5倍音も、実際の楽器の「ミ」や「ド#」の音とはほんの少しだけずれています。その理由やそれによる影響などは、後日別の記事としてアップしたいと思います)
マイナーコードの音は倍音に含まれない
8倍音以上の倍音も理論上は無数に存在します。8倍音は4倍音の2倍ですから、3オクターブ上の音になります。以降、16倍音や32倍音などの倍音は基音とオクターブの関係にあります。しかし、それらを除けばほとんどの倍音は、楽器で使われる12音階のいずれの音ともずれた音になります。
基音が「ラ」の時に、それの倍音で12音階の音とほぼ一致するものは、オクターブ音を除けば3倍音の「ミ」と5倍音の「ド#」しかありません(厳密にはこれらの音も1Hzほどずれているわけですが)。
ここで、ようやくマイナーコードの話になります。先ほどメジャーコードが基音、3倍音、5倍音の組み合わせだから心地よく聞こえる、と言いましたが、その逆で、「マイナーコードは倍音でない音が含まれているから暗く聞こえる」という推測がされているのです。
「推測」と言ったのは、以前の記事でも述べましたが、「倍音を含んだら心地よく感じ、倍音でない音があったら不快に感じる」という人間の耳(あるいは脳?)のメカニズム自体が本当かどうか明らかではないからです。
まとめ
今回は少し難しい話になってしまいました。特に、グラフの説明のあたりは嫌になって飛ばしてしまった方もいらっしゃるのではないでしょうか?正直、ここに述べたことは理解できなくても作曲はできますし、耳コピもできます。音楽理論を本気で勉強しないといけない人でない限り、知らなくても問題ないでしょう。でも、音楽をやっていると「倍音」って何?と聞かれることもあるかもしれません。その時にこの記事を思い出して、うまいこと説明できるくらいのネタ程度になってくれれば、苦労して記事を書いた甲斐があるというものです。

