前回のおさらい
当記事は、「平均律」と「純正律」に書いた記事の後編になります。全編は以下のリンク先を見ていただきたいのですが、簡単に概要をおさらいしたいと思います。
現在多くの音楽で使用されている音律は、「平均律」と言って、全ての音程の関係が同じ周波数の比率になるような音律です。平均律のメリットとしては、度数が同じ音程を奏でた場合、キーが何であっても同じ響きに感じるということです。デメリットとしては、平均律で奏でる和音は、その数学的な性質から、必ず「倍音」と周波数が少しだけずれてしまい、その結果「うなり」という現象を発生させるという事を述べました。
今回は、その「うなり」が理論上発生しない「純正律」のメリットとデメリットを述べたいと思います。
純正律とは?
純正率では、まず基準となる音階と、その最初の音の周波数を決めます。ここでは前回と同様、Aメジャーの音階を考えることにし、A5の周波数を880Hzとしておきましょう。ずいぶんいい加減に決めているように見えるかもしれませんが、基準となる音の高さは、理論的にはたいして重要ではありません(実際に楽器を調律するときは大事ですが、純正律と平均律の違いを説明するにあたっては重要ではない、という意味です)。したがって、ここは別に884Hzでも何でも構いません。A5を880Hzと定義すればA6が2倍の1760Hzになることも、平均律の場合と全く変わりありません。方法が異なるのは、A以外の音の周波数を決めるためのルールです。
平均律では各音の高さを、880Hzに対して2の12乗根をかけて求めていきましたが、純正律においては倍音の考え方を使って各音程を定義していきます。
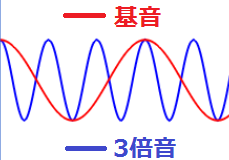
最初に音程を定義できるのはE6になります。E6という音は、A4(440Hz)の3倍音になります。したがって、E6の周波数は1320Hzとなります。この計算を、A5の880Hzを基準にしてみると、まず、周波数を半分にして3倍にした、ということが分かると思います。つまり、E6の周波数はA6の周波数に3/2を掛けることで得ることができます。
同じようにして、今度はC#の周波数も求められます。C#5という音は、A3(220Hz)の5倍音になります。A3はA5から見て2オクターブ下の音です。2オクターブ下ということは、周波数は1/4になるんでしたね。したがって、A5を基準にすればC#の周波数は、5/4をかけることで得ることができ、その数は1100Hzになります。
今度はD6を定義してみましょう。AからDを直接周波数を求めるのは難しいので、逆から考えてみましょう。D6から見ると、5度上の音はA6です。そして、先ほど5度上の音の周波数は、元の音の周波数に3/2を掛けることで得られると言いました。つまり、数式で書くと
(D6の周波数)×(3/2) = (A6の周波数)ということがわかります。ここで、(A6の周波数)=(A5の周波数)×2であることが分かっていますから、上の2つの式から、(D6の周波数)×(3/2)=(A5の周波数)×2となります。
これを整理すると、(D6の周波数)=(A5の周波数)×4/3となり、結局D6の音(すなわち元の音と4度の関係にある音)の周波数は、A5の周波数に4/3を掛ければ得られることが分かります。
このように、得られた音の周波数から、3倍音、5倍音等を組み合わせて計算すると、A5からA6までのメジャースケール上にある音の周波数を以下の様に得ることができます。
| 音名 | 純正律で計算した周波数 | 元の音の周波数に何を掛けたか |
| A5 | 880Hz | 1 |
| B5 | 990Hz | 9/8 |
| C6# | 1100Hz | 5/4 |
| D6 | 1173.3Hz | 4/3 |
| E6 | 1320Hz | 3/2 |
| F#6 | 1467Hz | 5/3 |
| G#6 | 1650Hz | 15/8 |
| A6 | 1760Hz | 2 |
以上のように、全ての音がA5の880Hzに対して、単純な分数をかけただけで周波数が求まることがわかります。平均律の場合は2の12乗根という複雑な無理数を使わないと求められなかったのとは対照的です。しかし、純正律の良いところは、何も計算が簡単なだけではありません。
これらの周波数はもともと、全て基音(もしくはそのオクターブの関係にある音)に対して3倍音や5倍音になるように周波数を決めてきました。ということは、この音律で定めた和音(コード)を奏でると、基音の倍音と、各構成音が完全に一致することになります。
たとえば、Aというコード(A,C#,E)を奏でることを考えてみましょう。その時、C#はAの5倍音の2オクターブ下と完全に一致するし、EはAの3倍音の1オクターブ下と、周波数は完全に一致します。ということは、この音律で調律された楽器で、Aのコードを弾いた場合、理論上「うなり」といわれる現象は起きないという事になります。このことから平均律は「理想的な音律」と呼ばれることもあり、これが平均律との決定的な違いです。
Aというコードの例で説明しましたが、これはDやEといった、Aメジャースケールのダイアトニックメジャーコードならばどれも同様です。
純正律の問題点
ここまで、純正律が「うなり」が発生しない理想的な音律である事を説明しましたが、それならば、なぜ現代では多くの音楽で「純正律」が採用されず、うなりが発生する「平均律」が採用されているのでしょうか?それは、純正律には、「移調、転調に向かない」という大きな問題点があるからなのです。
たとえば、上記の音律において、「A→E」という2音をの周波数比と、「B→F#」という2音の周波数比を考えてみましょう。これらはどちらも音楽理論で「完全五度」と呼ばれる音程で、平均律であればこれらの周波数比は完全に一致します。しかし、純正律では前者は上の表のとおり周波数比が3/2 (=1.5) になるのに対して、後者は(5/3) ÷ (9/8) = 1.48となり、わずかですが比率が違っています。つまり、同じ音程なのに、キーによって感じ方が異なってしまうのです。
それだけではありません。上の表を見た時に気づかれた方もいらっしゃるかもしれませんが、1オクターブの中に8個しか音がなく、例えば、CやD#といった音がないことに気づかれたでしょうか?実は、この理想的な音律と呼ばれる純正律は、音楽理論に忠実にのっとったコードや音のみを使うことを前提に考えられているため、現代の音楽のように、臨時調号や、ダイアトニック外のコードを多用する音楽には不向きなのです。
このことより、純正律では途中で転調する楽曲はほとんど演奏不可能です。なぜなら、ある調(キー)において、スケール上に存在する音しか周波数が定義できないのでは、それ以外の調の曲などを演奏できるはずはないからです。これは、1曲の中に複数の調が存在する場合だけに発生する問題ではありません。たとえば演奏会で2つの曲を連続して弾く場合、1曲目がAのキーの曲を演奏した場合、もし2曲目がA以外の曲だったら、曲ごとに再調律をしないと演奏ができなくなってしまうのです。
平均律と純正律、それぞれの良さを生かした利用法
ここで、それぞれの音律のメリットとデメリットをまとめてみましょう。
平均律は、12音全てが平等に扱われる音階なので、転調や移調などを自在に行うことができます。楽曲ごとに調律をする必要もありません。Aのキーの楽曲で正しく調律されていれば、Eのキーでも正しく演奏できることが保障されています。しかし、「うなり」が発生するという性質は本質的に防ぐことができません。このことから、「うなり」がそれほど目立たないように、多数の楽器が使われたオーケストラ、ポップス、ロックなどに向いている音律と言えます。楽器がたくさんあると仮にうなりが発生していても、あまりにも多くの種類の音があるためにほとんど意識できず、結果としそれほど不快感を感じないためです。
一方の純正律で構成された和音は、理論上「うなり」が発生しない綺麗な響きを与えます。しかし、使うことができるコードや音に限りがある上、あるキーのために調律された楽器は、他のキーの楽曲の演奏には使えないという問題点がありました。このため、少数の楽器を扱う音楽、あるいは楽器を全く使わない声楽に多く用いられます(人間の声はその場その場で周波数を変えることができるので、ある意味一番調律のしやすい「楽器」と言えます)。たとえば、オルガンと合唱のみからなる教会音楽は特殊なコードを使うこともほとんどなく、純正律の綺麗な和声を奏でることができるのです。歴史的に見ればむしろ純正律の方が先に開発され、平均律は後から出てきたものなのです。どちらが正しいというものではなく、状況に応じて使い分けられるべきものなのです。
まとめ
2記事にわたって、平均律、純正律という2種類の音律のそれぞれの性質と、メリット、デメリットについて説明してきました。特に純正律の方は我々の常識と異なる点が多く、なかなか理解しにくかったのではないかと思います。本記事ではそれぞれの音律において具体的な音源として提示することはしませんでしたが、ネット上を検索すれば2つの音律を聴き比べることができるサイトも多数存在しますので、ぜひ本記事で読んだことを念頭に置いたうえで、いろいろな音楽、音源を聴いていただくことをお勧めします。

